Deep Learning Book Series · 2.10 The Trace Operator
Introduction
I can assure you that you will read this chapter in 2 minutes! It is nice after the last two chapters that were quite big! We will see what is the Trace of a matrix. It will be needed for the last chapter on the Principal Component Analysis (PCA).
2.10 The Trace Operator
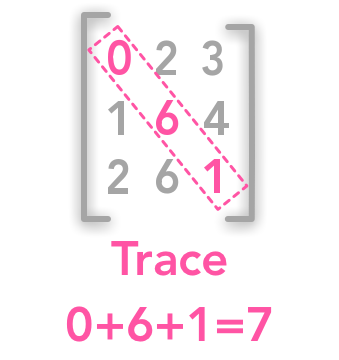The trace of matrix
The trace is the sum of all values in the diagonal of a square matrix.
$ \bs{A}= \begin{bmatrix} 2 & 9 & 8 \\ 4 & 7 & 1 \\ 8 & 2 & 5 \end{bmatrix} $
\(\mathrm{Tr}(\bs{A}) = 2 + 7 + 5 = 14\)
Numpy provides the function trace() to calculate it:
A = np.array([[2, 9, 8], [4, 7, 1], [8, 2, 5]])
A
array([[2, 9, 8],
[4, 7, 1],
[8, 2, 5]])
A_tr = np.trace(A)
A_tr
14
GoodFellow et al. explain that the trace can be used to specify the Frobenius norm of a matrix (see 2.5). The Frobenius norm is the equivalent of the $L^2$ norm for matrices. It is defined by:
\(\norm{\bs{A}}_F=\sqrt{\sum_{i,j}A^2_{i,j}}\)
Take the square of all elements and sum them. Take the square root of the result. This norm can also be calculated with:
\(\norm{\bs{A}}_F=\sqrt{\Tr({\bs{AA}^T})}\)
We can check this. The first way to compute the norm can be done with the simple command np.linalg.norm():
np.linalg.norm(A)
17.549928774784245
The Frobenius norm of $\bs{A}$ is 17.549928774784245.
With the trace the result is identical:
np.sqrt(np.trace(A.dot(A.T)))
17.549928774784245
Since the transposition of a matrix doesn’t change the diagonal, the trace of the matrix is equal to the trace of its transpose: \[\Tr(\bs{A})=\Tr(\bs{A}^T)\]
Trace of a product
\[\Tr(\bs{ABC}) = \Tr(\bs{CAB}) = \Tr(\bs{BCA})\]Example 1.
Let’s see an example of this property.
$ \bs{A}= \begin{bmatrix} 4 & 12 \\ 7 & 6 \end{bmatrix} $
$ \bs{B}= \begin{bmatrix} 1 & -3 \\ 4 & 3 \end{bmatrix} $
$ \bs{C}= \begin{bmatrix} 6 & 6 \\ 2 & 5 \end{bmatrix} $
A = np.array([[4, 12], [7, 6]])
B = np.array([[1, -3], [4, 3]])
C = np.array([[6, 6], [2, 5]])
np.trace(A.dot(B).dot(C))
531
np.trace(C.dot(A).dot(B))
531
np.trace(B.dot(C).dot(A))
531
$ \bs{ABC}= \begin{bmatrix} 360 & 432 \\ 180 & 171 \end{bmatrix} $
$ \bs{CAB}= \begin{bmatrix} 498 & 126 \\ 259 & 33 \end{bmatrix} $
$ \bs{BCA}= \begin{bmatrix} -63 & -54 \\ 393 & 594 \end{bmatrix} $
\(\Tr(\bs{ABC}) = \Tr(\bs{CAB}) = \Tr(\bs{BCA}) = 531\)
References
Feel free to drop me an email or a comment. The syllabus of this series can be found in the introduction post. All the notebooks can be found on Github.
This content is part of a series following the chapter 2 on linear algebra from the Deep Learning Book by Goodfellow, I., Bengio, Y., and Courville, A. (2016). It aims to provide intuitions/drawings/python code on mathematical theories and is constructed as my understanding of these concepts. You can check the syllabus in the introduction post.
