Essential Math for Data Science Update

I’m glad to announce a few updates concerning my book Essential Math for Data Science.

First, I changed the structure of the book: a first chapter on basic algebra has been removed. Part of old chapter 02 has been merged in the linear algebra part.
I restructured the table of content: I removed some content about very basic math (like what is an equation or a function) to have more space to cover slighly more advanced contents. The part Statistics and Probability is now at the beginning of the book (just after a first part on Calculus). Have a look at the new TOC below to have more details.
There is now hands-on projects for each chapter. Hands-on projects are sections where you can apply the math you just learned to a practical machine learning problem (like gradient descent or regularization, for instance). The difficulty of math and code in each of these hands-on project is variable, so you should find something at the right point of your learning curve.

Here is the table of content. Click on the chapters to see what’s inside.

Table of Content

01. How to use this Book

PART 1. Calculus

Machine learning and data science require some experience with calculus. You’ll be introduced here to derivatives and integrals and how they are useful in machine learning and data science.

02. Calculus: Derivatives and Integrals
$Area under the curve$ Area under the curve
- 2.1 Derivatives
  2.1.1 Introduction
  2.1.2 Mathematical Definition of Derivatives
  2.1.3 Derivatives of Linear And Nonlinear Functions
  2.1.4 Derivative Rules
  2.1.5 Partial Derivatives And Gradients
- 2.2 Integrals And Area Under The Curve
  2.2.1 Example
  2.2.2 Riemann Sum
  2.2.3 Mathematical Definition
- 2.3 Hands-On Project: Gradient Descent
  2.3.1 Cost function
  2.3.2 Derivative of the Cost Function
  2.3.3 Implementing Gradient Descent
  2.3.4 MSE Cost Function With Two Parameters

PART 2. Statistics and Probability

In machine learning and data science, probability and statistics are used to deal with uncertainty. This uncertainty comes from various sources, from data collection to the process you’re trying to model itself. This part will introduce you to descriptive statistics, probability distributions, bayesian statistics and information theory.

03. Statistics and Probability Theory
$Joint and Marginal Probability$ Joint and Marginal Probability
- 3.1 Descriptive Statistics
  3.1.1 Variance and Standard Deviation
  3.1.2 Covariance and Correlation
  3.1.3 Covariance Matrix
- 3.2 Random Variables
  3.2.1 Definitions and Notation
  3.2.2 Discrete and Continuous Random Variables
- 3.3 Probability Distributions
  3.3.1 Probability Mass Functions
  3.3.2 Probability Density Functions
  2.3.3 Implementing Gradient Descent
  2.3.4 MSE Cost Function With Two Parameters
- 3.4 Joint, Marginal, and Conditional Probability
  3.4.1 Joint Probability
  3.4.2 Marginal Probability
  3.4.3 Conditional Probability
- 3.5 Cumulative Distribution Functions
- 3.6 Expectation and Variance of Random Variables
  3.6.1 Discrete Random Variables
  3.6.2 Continuous Random Variables
  3.6.3 Variance of Random Variables
- 3.7 Hands-On Project: The Central Limit Theorem
  3.7.1 Continuous Distribution
  3.7.2 Discrete Distribution
04. Common Probability Distributions
$Gaussian Distributions$ Gaussian Distributions
- 4.1 Uniform Distribution
- 4.2 Gaussian distribution
  4.2.1 Formula
  4.2.2 Parameters
  4.2.3 Requirements
- 4.3 Bernoulli Distribution
- 4.4 Binomial Distribution
  4.4.1 Description
  4.4.2 Graphical Representation
- 4.5 Poisson Distribution
  4.5.1 Mathematical Definition
  4.5.2 Example
- 4.6 Exponential Distribution
  4.6.1 Derivation from the Poisson Distribution
  4.6.2 Effect of λ
- 4.7 Hands-on Project: Waiting for the Bus
05. Bayesian Statistics and Information Theory
$Bayesian Inference$ Bayesian Inference
- 5.1 Bayes’ Theorem
  5.1.1 Mathematical Formulation
  5.1.2 Example
  5.1.3 Bayesian Interpretation
  5.1.4 Bayes’ Theorem with Distributions
- 5.2 Likelihood
  5.2.1 Introduction and Notation
  5.2.2 Finding the Parameters of the Distribution
  5.2.3 Maximum Likelihood Estimation
- 5.3 Information Theory
  5.3.1 Shannon Information
  5.3.2 Entropy
  5.3.3 Cross Entropy
  5.3.4 Kullback-Leibler Divergence (KL Divergence)
- 5.4 Hands-On Project: Bayesian Inference
  5.4.1 Advantages of Bayesian Inference
  5.4.2 Project

PART 3. Linear Algebra

Linear algebra is the core of many machine learning algorithms. The great news is that you don’t need to be able to code these algorithms yourself. It is more likely that you’ll use a great Python library instead. However, to be able to choose the right model for the right job, or to debug a broken machine learning pipeline, it is crucial to have enough understanding of what’s under the hood. The goal of this part is to give you enough understanding and intuition about the major concepts of linear algebra used in machine and data science. It is designed to be accessible, even if you never studied linear algebra.

06. Scalars and Vectors
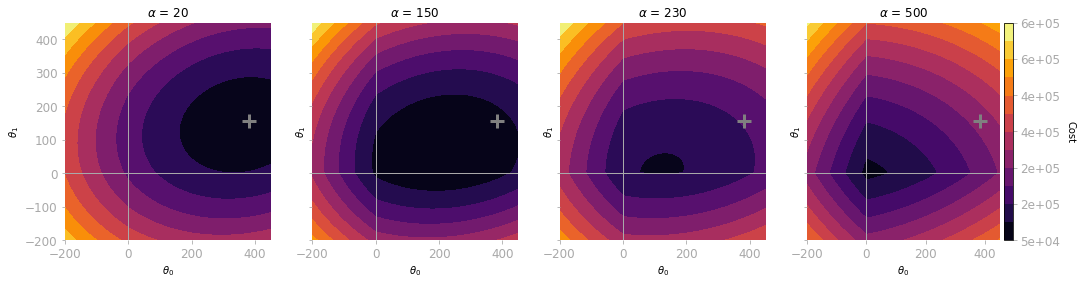$L1 Regularization. Effect of Lambda.$ L1 Regularization. Effect of Lambda.
- 6.1 What Vectors are?
  6.1.1 Geometric and Coordinate Vectors
  6.1.2 Vector Spaces
  6.1.3 Special Vectors
- 6.2 Operations and Manipulations on Vectors
  6.2.1 Scalar Multiplication
  6.2.2 Vector Addition
  6.2.3 Transposition
- 6.3 Norms
  6.3.1 Definitions
  6.3.2 Common Vector Norms
  6.3.3 Norm Representations
- 6.4 The Dot Product
  6.4.1 Definition
  6.4.2 Geometric interpretation: Projections
  6.4.3 Properties
- 6.5 Hands-on Project: Regularization
  6.5.1 Introduction
  6.5.2 Effect of Regularization on Polynomial Regression
  6.5.3 Differences between $L^1$ and $L^2$ Regularization
07. Matrices and Tensors
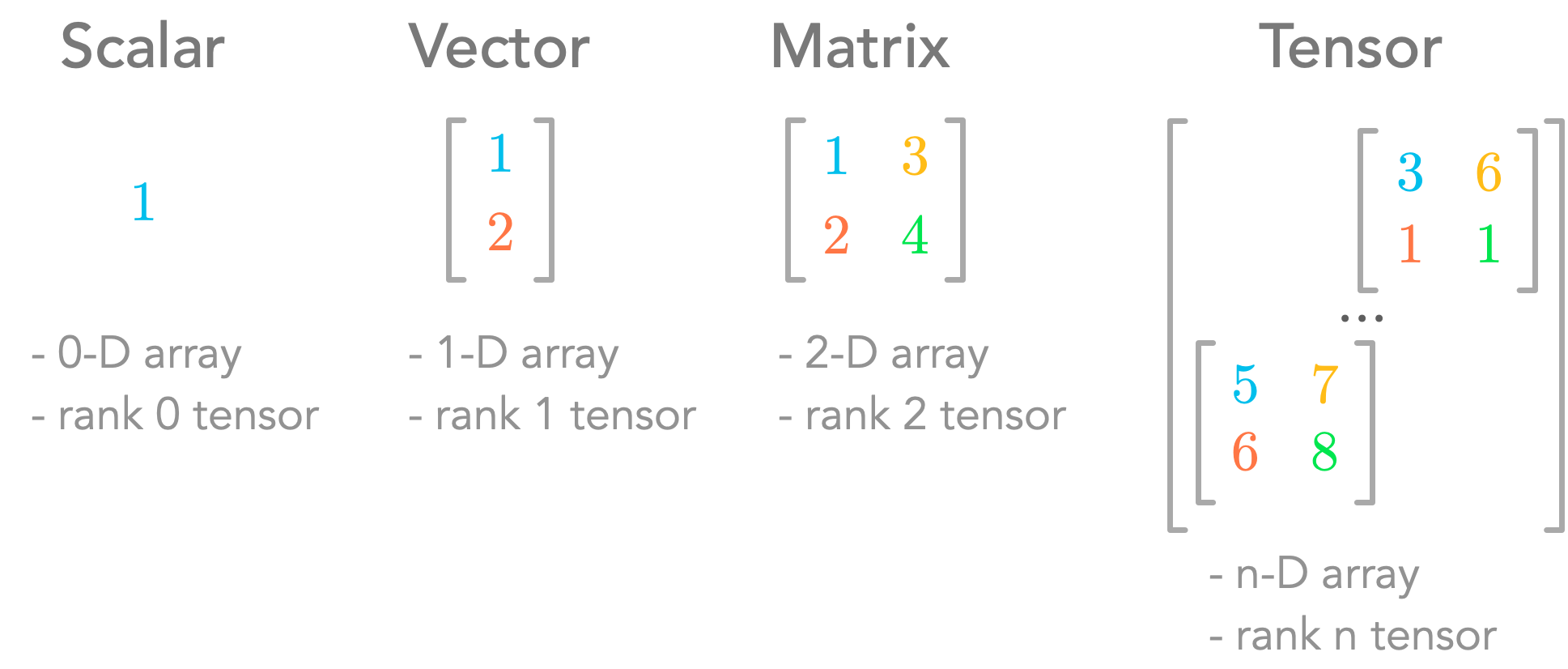$Scalars, vectors, matrices and tensors$ Scalars, vectors, matrices and tensors
- 7.1 Introduction
  7.1.1 Matrix Notation
  7.1.2 Shapes
  7.1.3 Indexing
  7.1.4 Main Diagonal
  7.1.5 Tensors
  7.1.6 Frobenius Norm
- 7.2 Operations and Manipulations on Matrices
  7.2.1 Addition and Scalar Multiplication
  7.2.2 Transposition
- 7.3 Matrix Product
  7.3.1 Matrices with Vectors
  7.3.2 Matrices Product
  7.3.3 Transpose of a Matrix Product
- 7.4 Special Matrices
  7.4.1 Square Matrices
  7.4.2 Diagonal Matrices
  7.4.3 Identity Matrices
  7.4.4 Inverse Matrices
  7.4.5 Orthogonal Matrices
  7.4.6 Symmetric Matrices
  7.4.7 Triangular Matrices
- 7.5 Hands-on Project: Image Classifier
  7.5.1 Images as Multi-dimensional Arrays
  7.5.2 Data Preparation
08. Span, Linear Dependency, and Space Transformation
$Linear Combination$ All linear Combinations of two vectors
- 8.1 Linear Transformations
  8.1.1 Intuition
  8.1.2 Linear Transformations as Vectors and Matrices
  8.1.3 Geometric Interpretation
  8.1.4 Special Cases
- 8.2 Linear combination
  8.2.1 Intuition
  8.2.2 All combinations of vectors
  8.2.3 Span
- 8.3 Subspaces
  8.3.1 Definitions
  8.3.2 Subspaces of a Matrix
- 8.4 Linear dependency
  8.4.1 Geometric Interpretation
  8.4.2 Matrix View
- 8.5 Basis
  8.5.1 Definitions
  8.5.2 Linear Combination of Basis Vectors
  8.5.3 Other Bases
- 8.6 Special Characteristics
  8.6.1 Rank
  8.6.2 Trace
  8.6.3 Determinant
- 8.7 Hands-On Project: Span
09. Systems of Linear Equations
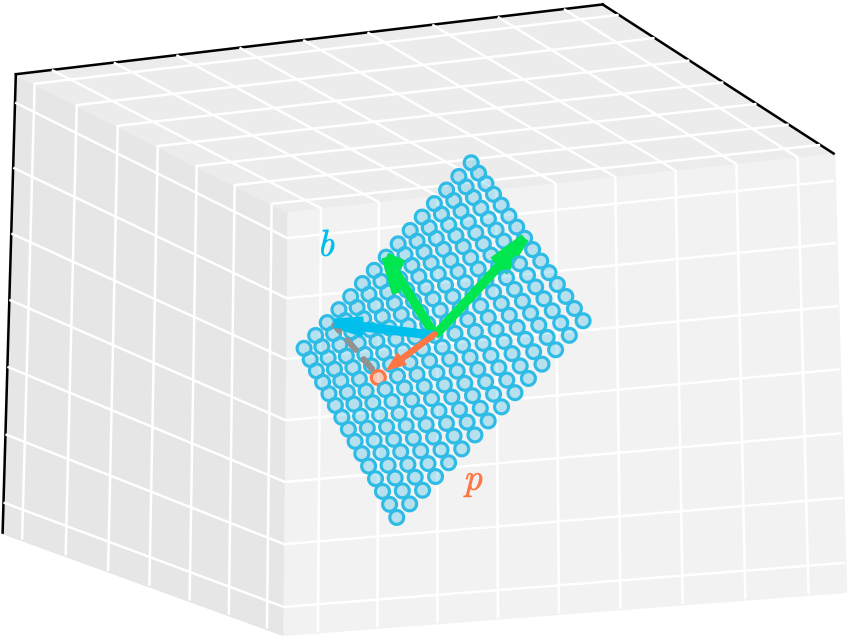$Projection of a vector onto a plane$ Projection of a vector onto a plane
- 9.1 System of linear equations
  9.1.1 Row Picture
  9.1.2 Column Picture
  9.1.3 Number of Solutions
  9.1.4 Representation of Linear Equations With Matrices
- 9.2 System Shape
  9.2.1 Overdetermined Systems of Equations
  9.2.2 Underdetermined Systems of Equations
- 9.3 Projections
  9.3.1 Solving Systems of Equations
  9.3.2 Projections to Approximate Unsolvable Systems
  9.3.3 Projections Onto a Line
  9.3.4 Projections Onto a Plane
- 9.4 Hands-on Project: Linear Regression Using Least Approximation
  9.4.1 Linear Regression Using the Normal Equation
  9.4.2 Relationship Between Least Squares and the Normal Equation
10. Eigenvectors and Eigenvalues
$Principal Component Analysis on audio samples.$ Principal Component Analysis on audio samples.
- 10.1 Eigenvectors and Linear Transformations
- 10.2 Change of Basis
  10.2.1 Linear Combinations of the Basis Vectors
  10.2.2 The Change of Basis Matrix
  10.2.3 Example: Changing the Basis of a Vector
- 10.3 Linear Transformations in Different Bases
  10.3.1 Transformation Matrix
  10.3.2 Transformation Matrix in Another Basis
  10.3.3 Interpretation
- 10.4 Eigendecomposition
  10.4.1 First Step: Change of Basis
  10.4.2 Eigenvectors and Eigenvalues
  10.4.3 Diagonalization
  10.4.4 Eigendecomposition of Symmetric Matrices
- 10.5 Hands-On Project: Principal Component Analysis
  10.5.1 Under the Hood
  10.5.2 Making Sense of Audio
11. Singular Value Decomposition
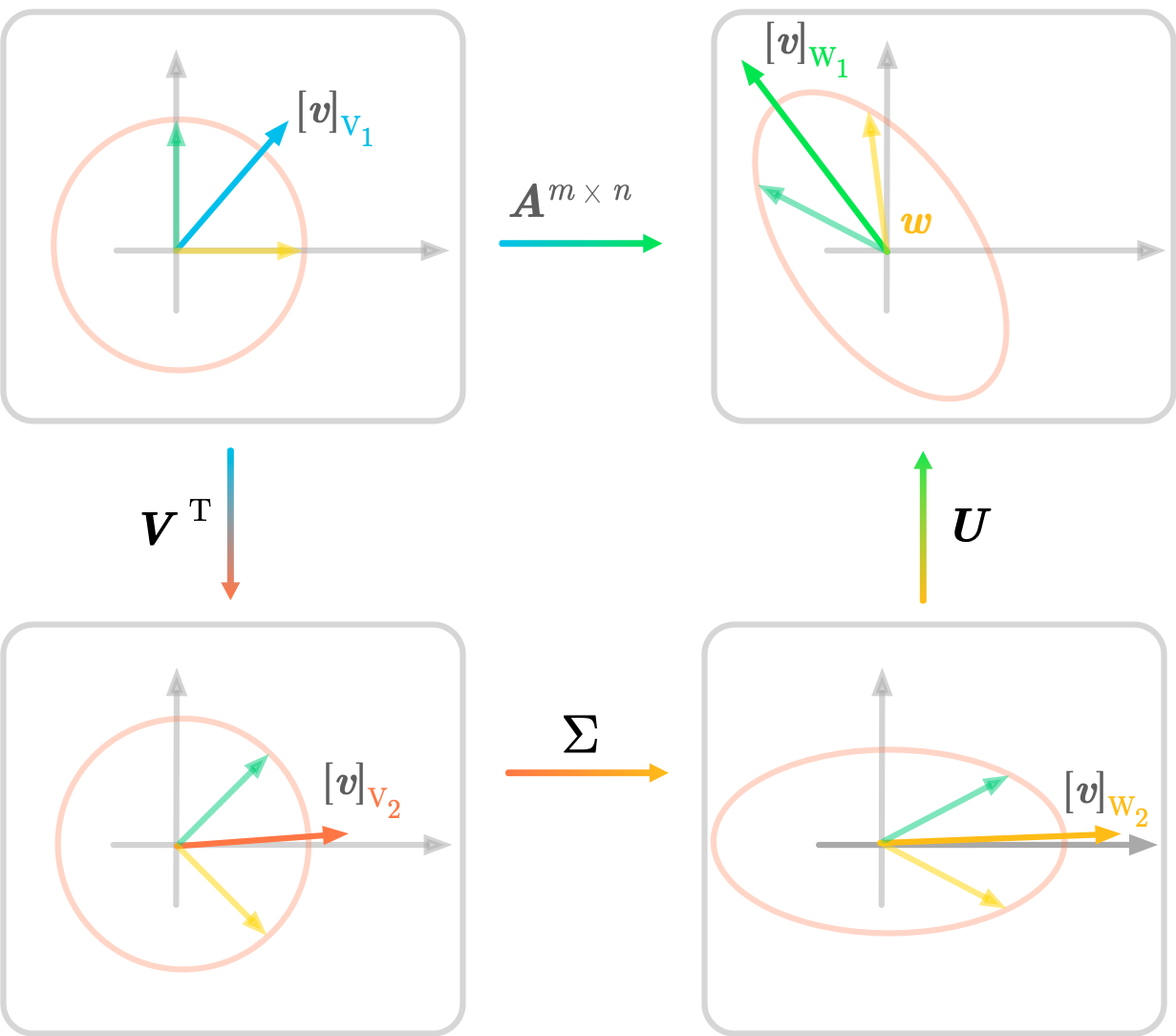$SVD Geometry$ SVD Geometry
- 11.1 Nonsquare Matrices
  11.1.1 Different Input and Output Spaces
  11.1.2 Specifying the Bases
  11.1.3 Eigendecomposition is Only for Square Matrices
- 11.2 Expression of the SVD
  11.2.1 From Eigendecomposition to SVD
  11.2.2 Singular Vectors and Singular Values
  11.2.3 Finding the Singular Vectors and the Singular Values
  11.2.4 Summary
- 11.3 Geometry of the SVD
  11.3.1 Two-Dimensional Example
  11.3.2 Comparison with Eigendecomposition
  11.3.3 Three-Dimensional Example
  11.3.4 Summary
- 11.4 Low-Rank Matrix Approximation
  11.4.1 Full SVD, Thin SVD and Truncated SVD
  11.4.2 Decomposition into Rank One Matrices
- 11.5 Hands-On Project: Image Compression