Last update: May 2020

Introduction

The dot product is a major concept of linear algebra and thus machine learning and data science. We will see some properties of this operation. Then, we will get some intuition on the link between matrices and systems of linear equations.

2.2 Multiplying Matrices and Vectors

The standard way to multiply matrices is not to multiply each element of one with each element of the other (called the element-wise product) but to calculate the sum of the products between rows and columns. The matrix product, also called dot product, is calculated as following:

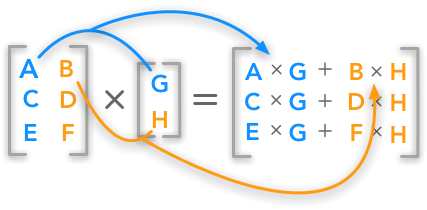An example of how to calculate the dot product between a matrix and a vector The dot product between a matrix and a vector

The number of columns of the first matrix must be equal to the number of rows of the second matrix. If the dimensions of the first matrix is ($m \times n$), the second matrix needs to be of shape ($n \times x$). The resulting matrix will have the shape ($m \times x$).

Example 1.

Let’s start with the multiplication of a matrix and a vector.

$ \bs{A} \times \bs{b} = \bs{C} $

with:

$ \bs{A}= \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix} $

and:

$ \bs{b}=\begin{bmatrix} 2\\ 4 \end{bmatrix} $

We saw that the formula is the following:

$ \begin{aligned} &\begin{bmatrix} A_{1,1} & A_{1,2} \\ A_{2,1} & A_{2,2} \\ A_{3,1} & A_{3,2} \end{bmatrix}\times \begin{bmatrix} B_{1,1} \\ B_{2,1} \end{bmatrix}=\\ &\begin{bmatrix} A_{1,1}B_{1,1} + A_{1,2}B_{2,1} \\ A_{2,1}B_{1,1} + A_{2,2}B_{2,1} \\ A_{3,1}B_{1,1} + A_{3,2}B_{2,1} \end{bmatrix} \end{aligned} $

So we will have:

$ \begin{aligned} &\begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix}\times \begin{bmatrix} 2 \\ 4 \end{bmatrix}=\\ &\begin{bmatrix} 1 \times 2 + 2 \times 4 \\ 3 \times 2 + 4 \times 4 \\ 5 \times 2 + 6 \times 4 \end{bmatrix}= \begin{bmatrix} 10 \\ 22 \\ 34 \end{bmatrix} \end{aligned} $

It is a good habit to check the dimensions of the matrix to see what is going on. We can see in this example that the shape of $\bs{A}$ is ($3 \times 2$) and the shape of $\bs{b}$ is ($2 \times 1$). So the dimensions of $\bs{C}$ are ($3 \times 1$).

With Numpy

The Numpy function dot() can be used to compute the matrix product (or dot product). Let’s try to reproduce the last exemple:

A = np.array([[1, 2], [3, 4], [5, 6]])
A

array([[1, 2],
       [3, 4],
       [5, 6]])

B = np.array([[2], [4]])
B

array([[2],
       [4]])

C = np.dot(A, B)
C

array([[10],
       [22],
       [34]])

It is equivalent to use the method dot() of Numpy arrays:

C = A.dot(B)
C

array([[10],
       [22],
       [34]])

Example 2.

Multiplication of two matrices.

$\bs{A} \bs{B} = \bs{C}$

with:

$\bs{A}=\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ 10 & 11 & 12 \end{bmatrix} $

and:

$\bs{B}=\begin{bmatrix} 2 & 7 \\ 1 & 2 \\ 3 & 6 \end{bmatrix} $

So we have:

$ \begin{aligned} &\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ 10 & 11 & 12 \end{bmatrix} \begin{bmatrix} 2 & 7 \\ 1 & 2 \\ 3 & 6 \end{bmatrix}=\\ &\begin{bmatrix} 2 \times 1 + 1 \times 2 + 3 \times 3 & 7 \times 1 + 2 \times 2 + 6 \times 3 \\ 2 \times 4 + 1 \times 5 + 3 \times 6 & 7 \times 4 + 2 \times 5 + 6 \times 6 \\ 2 \times 7 + 1 \times 8 + 3 \times 9 & 7 \times 7 + 2 \times 8 + 6 \times 9 \\ 2 \times 10 + 1 \times 11 + 3 \times 12 & 7 \times 10 + 2 \times 11 + 6 \times 12 \\ \end{bmatrix}\\ &= \begin{bmatrix} 13 & 29 \\ 31 & 74 \\ 49 & 119 \\ 67 & 164 \end{bmatrix} \end{aligned} $

Let’s check the result with Numpy:

A = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]])
A

array([[ 1,  2,  3],
       [ 4,  5,  6],
       [ 7,  8,  9],
       [10, 11, 12]])

B = np.array([[2, 7], [1, 2], [3, 6]])
B

array([[2, 7],
       [1, 2],
       [3, 6]])

C = A.dot(B)
C

array([[ 13,  29],
       [ 31,  74],
       [ 49, 119],
       [ 67, 164]])

It works!

Formalization of the dot product

The dot product can be formalized through the following equation:

$ C_{i,j} = A_{i,k}B_{k,j} = \sum_{k}A_{i,k}B_{k,j} $

You can find more examples about the dot product here.

Properties of the dot product

We will now see some interesting properties of the dot product. Using simple examples for each property, we’ll get used to the Numpy functions.

Simplification of the matrix product

$(\bs{AB})^{\text{T}} = \bs{B}^\text{T}\bs{A}^\text{T}$

A = np.array([[2, 3], [1, 4], [7, 6]])
A

array([[2, 3],
       [1, 4],
       [7, 6]])

B = np.array([[5, 3], [2, 2]])
B

array([[5, 3],
       [2, 2]])

$(\bs{AB})^{\text{T}}$:

AB_t = A.dot(B).T
AB_t

array([[16, 13, 47],
       [12, 11, 33]])

is equivalent to $\bs{B}^\text{T}\bs{A}^\text{T}$:

B_tA = B.T.dot(A.T)
B_tA

array([[16, 13, 47],
       [12, 11, 33]])

Matrix mutliplication is distributive

$\bs{A}(\bs{B}+\bs{C}) = \bs{AB}+\bs{AC}$

Example 3.

$ \bs{A}=\begin{bmatrix} 2 & 3 \\ 1 & 4 \\ 7 & 6 \end{bmatrix}, \bs{B}=\begin{bmatrix} 5 \\ 2 \end{bmatrix}, \bs{C}=\begin{bmatrix} 4 \\ 3 \end{bmatrix} $

$ \begin{aligned} \bs{A}(\bs{B}+\bs{C})&=\begin{bmatrix} 2 & 3 \\ 1 & 4 \\ 7 & 6 \end{bmatrix}\times \left(\begin{bmatrix} 5 \\ 2 \end{bmatrix}+ \begin{bmatrix} 4 \\ 3 \end{bmatrix}\right)= \begin{bmatrix} 2 & 3 \\ 1 & 4 \\ 7 & 6 \end{bmatrix}\times \begin{bmatrix} 9 \\ 5 \end{bmatrix}\\ &= \begin{bmatrix} 2 \times 9 + 3 \times 5 \\ 1 \times 9 + 4 \times 5 \\ 7 \times 9 + 6 \times 5 \end{bmatrix}= \begin{bmatrix} 33 \\ 29 \\ 93 \end{bmatrix} \end{aligned} $

is equivalent to

$ \begin{aligned} \bs{A}\bs{B}+\bs{A}\bs{C} &= \begin{bmatrix} 2 & 3 \\ 1 & 4 \\ 7 & 6 \end{bmatrix}\times \begin{bmatrix} 5 \\ 2 \end{bmatrix}+ \begin{bmatrix} 2 & 3 \\ 1 & 4 \\ 7 & 6 \end{bmatrix}\times \begin{bmatrix} 4 \\ 3 \end{bmatrix}\\ &= \begin{bmatrix} 2 \times 5 + 3 \times 2 \\ 1 \times 5 + 4 \times 2 \\ 7 \times 5 + 6 \times 2 \end{bmatrix}+ \begin{bmatrix} 2 \times 4 + 3 \times 3 \\ 1 \times 4 + 4 \times 3 \\ 7 \times 4 + 6 \times 3 \end{bmatrix}\\ &= \begin{bmatrix} 16 \\ 13 \\ 47 \end{bmatrix}+ \begin{bmatrix} 17 \\ 16 \\ 46 \end{bmatrix}= \begin{bmatrix} 33 \\ 29 \\ 93 \end{bmatrix} \end{aligned} $

A = np.array([[2, 3], [1, 4], [7, 6]])
A

array([[2, 3],
       [1, 4],
       [7, 6]])

B = np.array([[5], [2]])
B

array([[5],
       [2]])

C = np.array([[4], [3]])
C

array([[4],
       [3]])

$\bs{A}(\bs{B}+\bs{C})$:

D = A.dot(B+C)
D

array([[33],
       [29],
       [93]])

is equivalent to $\bs{AB}+\bs{AC}$:

D = A.dot(B) + A.dot(C)
D

array([[33],
       [29],
       [93]])

Matrix mutliplication is associative

$\bs{A}(\bs{BC}) = (\bs{AB})\bs{C}$

A = np.array([[2, 3], [1, 4], [7, 6]])
A

array([[2, 3],
       [1, 4],
       [7, 6]])

B = np.array([[5, 3], [2, 2]])
B

array([[5, 3],
       [2, 2]])

$\bs{A}(\bs{BC})$:

D = A.dot(B.dot(C))
D

array([[100],
       [ 85],
       [287]])

is equivalent to $(\bs{AB})\bs{C}$:

D = (A.dot(B)).dot(C)
D

array([[100],
       [ 85],
       [287]])

Matrix multiplication is not commutative

$\bs{AB} \neq \bs{BA}$

A = np.array([[2, 3], [6, 5]])
A

array([[2, 3],
       [6, 5]])

B = np.array([[5, 3], [2, 2]])
B

array([[5, 3],
       [2, 2]])

$\bs{AB}$:

AB = np.dot(A, B)
AB

array([[16, 12],
       [40, 28]])

is different from $\bs{BA}$:

BA = np.dot(B, A)
BA

array([[28, 30],
       [16, 16]])

However vector multiplication is commutative

$\bs{x^{ \text{T}}y} = \bs{y^{\text{T}}x} $

Let’s try with the following example:

x = np.array([[2], [6]])
x

array([[2],
       [6]])

y = np.array([[5], [2]])
y

array([[5],
       [2]])

$\bs{x^\text{T}y}$:

x_ty = x.T.dot(y)
x_ty

array([[22]])

is equivalent to $\bs{y^\text{T}x}$:

y_tx = y.T.dot(x)
y_tx

array([[22]])

One way to see why the vector multiplication is commutative is to notice that the result of $\bs{x^{ \text{T}}y}$ is a scalar. We know that scalars are equal to their own transpose, so mathematically, we have:

$\bs{x^{\text{T}}y} = (\bs{x^{\text{T}}y})^{\text{T}} = \bs{ y^{\text{T}} (x^{\text{T}})^{\text{T}} } = \bs{y^{\text{T}}x}$

System of linear equations

This is an important part of why linear algebra can be very useful to solve a large variety of problems. Here we will see that it can be used to represent systems of equations.

A system of equations is a set of multiple equations (at least 1). For instance we could have:

$ \begin{cases} y = 2x + 1 \\ y = \frac{7}{2}x +3 \end{cases} $

It is defined by its number of equations and its number of unknowns. In this example, there are 2 equations (the first and the second line) and 2 unknowns ($x$ and $y$). In addition we call this a system of linear equations because each equation is linear. We can represent that in 2 dimensions: we have one straight line per equation and dimensions correspond to the unknowns. Here is the plot of the first equation:

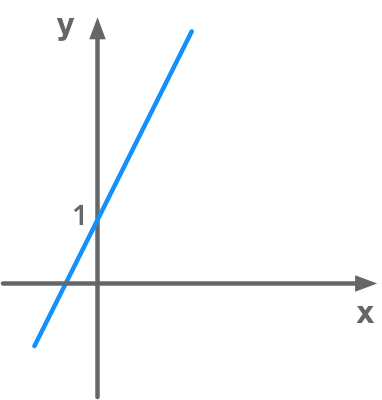Representation of a line from an equation Representation of a linear equation

In our system of equations, the unknowns are the dimensions and the number of equations is the number of lines (in 2D) or $n$-dimensional planes.

Using matrices to describe the system

Matrices can be used to describe a system of linear equations of the form $\bs{Ax}=\bs{b}$. Here is such a system:

$ A_{1,1}x_1 + A_{1,2}x_2 + A_{1,n}x_n = b_1 \\ A_{2,1}x_1 + A_{2,2}x_2 + A_{2,n}x_n = b_2 \\ \cdots \\ A_{m,1}x_1 + A_{m,2}x_2 + A_{m,n}x_n = b_n $

The unknowns (what we want to find to solve the system) are the variables $x_1$ and $x_2$. It is exactly the same form as with the last example but with all the variables on the same side. $y = 2x + 1$ becomes $-2x + y = 1$ with $x$ corresponding to $x_1$ and $y$ corresponding to $x_2$. We will have $n$ unknowns and $m$ equations.

The variables are named $x_1, x_2, \cdots, x_n$ by convention because we will see that it can be summarised in the vector $\bs{x}$.

Left-hand side

The left-hand side can be considered as the product of a matrix $\bs{A}$ containing weights for each variable ($n$ columns) and each equation ($m$ rows):

$ \bs{A}= \begin{bmatrix} A_{1,1} & A_{1,2} & \cdots & A_{1,n} \\ A_{2,1} & A_{2,2} & \cdots & A_{2,n} \\ \cdots & \cdots & \cdots & \cdots \\ A_{m,1} & A_{m,2} & \cdots & A_{m,n} \end{bmatrix} $

with a vector $\bs{x}$ containing the $n$ unknowns

$ \bs{x}= \begin{bmatrix} x_1 \\ x_2 \\ \cdots \\ x_n \end{bmatrix} $

The dot product of $\bs{A}$ and $\bs{x}$ gives a set of equations. Here is a simple example:

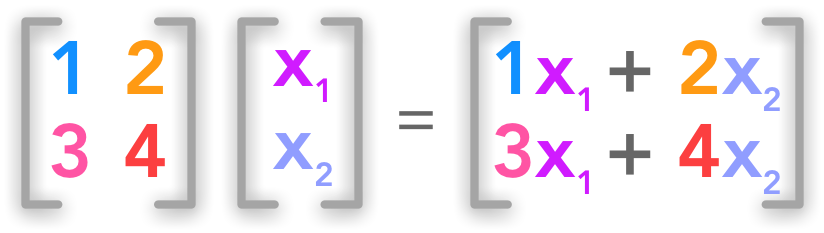Matrix form of a system of linear equation Matrix form of a system of linear equations

We have a set of two equations with two unknowns. So the number of rows of $\bs{A}$ gives the number of equations and the number of columns gives the number of unknowns.

Both sides

The equation system can be wrote like that:

$ \begin{bmatrix} A_{1,1} & A_{1,2} & \cdots & A_{1,n} \\ A_{2,1} & A_{2,2} & \cdots & A_{2,n} \\ \cdots & \cdots & \cdots & \cdots \\ A_{m,1} & A_{m,2} & \cdots & A_{m,n} \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ \cdots \\ x_n \end{bmatrix} = \begin{bmatrix} b_1 \\ b_2 \\ \cdots \\ b_m \end{bmatrix} $

Or simply:

$\bs{Ax}=\bs{b}$

Example 4.

We will try to convert the common form of a linear equation $y=ax+b$ to the matrix form. If we want to keep the previous notation we will have instead:

$x_2=ax_1+b$

Don’t confuse the variable $x_1$ and $x_2$ with the vector $\bs{x}$. This vector contains all the variables of our equations:

$ \bs{x} = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} $

In this example we will use the following equation:

$ \begin{aligned} &x_2=2x_1+1 \\ \Leftrightarrow& 2x_1-x_2=-1 \end{aligned} $

In order to end up with this system when we multiply $\bs{A}$ and $\bs{x}$ we need $\bs{A}$ to be a matrix containing the weights of each variable. The weight of $x_1$ is $2$ and the weights of $x_2$ is $-1$:

$ \bs{A}= \begin{bmatrix} 2 & -1 \end{bmatrix} $

So we have

$ \begin{bmatrix} 2 & -1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} 2x_1-1x_2 \end{bmatrix} $

To complete the equation we have

$ \bs{b}= \begin{bmatrix} -1 \end{bmatrix} $

which gives

$ \begin{bmatrix} 2 & -1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} -1 \end{bmatrix} $

This system of equations is thus very simple and contains only 1 equation ($\bs{A}$ has 1 row) and 2 variables ($\bs{A}$ has 2 columns).

To summarise, $\bs{A}$ will be a matrix of dimensions $m\times n$ containing scalars multiplying these variables (here $x_1$ is multiplied by 2 and $x_2$ by -1). The vector $\bs{x}$ contains the variables $x_1$ and $x_2$. And the right-hand side is the constant $\bs{b}$:

$ \bs{A}= \begin{bmatrix} 2 & -1 \end{bmatrix} $

$ \bs{x}= \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} $

$ \bs{b}= \begin{bmatrix} -1 \end{bmatrix} $

We can write this system

$ \bs{Ax}=\bs{b} $

We will see at the end of the the next chapter that this compact way of writing sets of linear equations can be very usefull. It provides a way to solve the equations.

References

Feel free to drop me an email or a comment. The syllabus of this series can be found in the introduction post. All the notebooks can be found on Github.

This content is part of a series following the chapter 2 on linear algebra from the Deep Learning Book by Goodfellow, I., Bengio, Y., and Courville, A. (2016). It aims to provide intuitions/drawings/python code on mathematical theories and is constructed as my understanding of these concepts. You can check the syllabus in the introduction post.

✠  Previous Deep Learning Book Series · 2.1 Scalars Vectors Matrices and Tensors ✠  Next Deep Learning Book Series · 2.3 Identity and Inverse Matrices