Deep Learning Book Series · 2.6 Special Kinds of Matrices and Vectors
Introduction
We have seen in 2.3 some interesting kind of matrices. We will see other type of vectors and matrices in this chapter. It is not a big chapter but it is important to understand the next ones.
2.6 Special Kinds of Matrices and Vectors
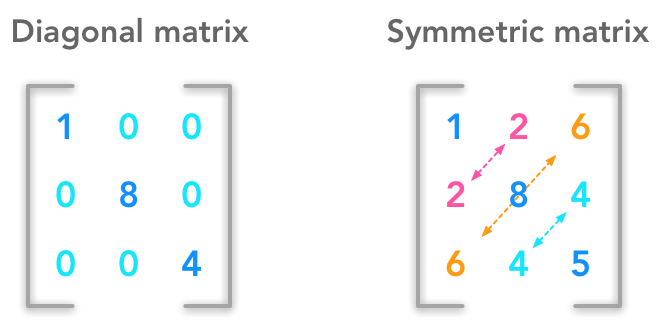Example of diagonal and symmetric matrices
Diagonal matrices
Example of a diagonal matrix
A matrix $\bs{A}_{i,j}$ is diagonal if its entries are all zeros except on the diagonal (when $i=j$).
Example 1.
$ \bs{D}= \begin{bmatrix} 2 & 0 & 0 & 0 \\ 0 & 4 & 0 & 0 \\ 0 & 0 & 3 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} $
Example 2.
In this case the matrix is also square but there can be non square diagonal matrices.
$ \bs{D}= \begin{bmatrix} 2 & 0 & 0 \\ 0 & 4 & 0 \\ 0 & 0 & 3 \\ 0 & 0 & 0 \end{bmatrix} $
Or
$ \bs{D}= \begin{bmatrix} 2 & 0 & 0 & 0 \\ 0 & 4 & 0 & 0 \\ 0 & 0 & 3 & 0 \end{bmatrix} $
Example 3.
The diagonal matrix can be denoted $diag(\bs{v})$ where $\bs{v}$ is the vector containing the diagonal values.
$ \bs{D}= \begin{bmatrix} 2 & 0 & 0 & 0 \\ 0 & 4 & 0 & 0 \\ 0 & 0 & 3 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} $
In this matrix, $\bs{v}$ is the following vector:
$ \bs{v}= \begin{bmatrix} 2 \\ 4 \\ 3 \\ 1 \end{bmatrix} $
The Numpy function diag() can be used to create square diagonal matrices:
v = np.array([2, 4, 3, 1])
np.diag(v)
array([[2, 0, 0, 0],
[0, 4, 0, 0],
[0, 0, 3, 0],
[0, 0, 0, 1]])
Example 4.
The mutliplication between a diagonal matrix and a vector is thus just a ponderation of each element of the vector by $v$:
$ \bs{D}= \begin{bmatrix} 2 & 0 & 0 & 0 \\ 0 & 4 & 0 & 0 \\ 0 & 0 & 3 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} $
and
$ \bs{x}= \begin{bmatrix} 3 \\ 2 \\ 2 \\ 7 \end{bmatrix} $
$ \begin{aligned} \bs{Dx}&= \begin{bmatrix} 2 & 0 & 0 & 0 \\ 0 & 4 & 0 & 0 \\ 0 & 0 & 3 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} 3 \\ 2 \\ 2 \\ 7 \end{bmatrix} \\ &=\begin{bmatrix} 2\times3 + 0\times2 + 0\times2 + 0\times7 \\ 0\times3 + 4\times2 + 0\times2 + 0\times7 \\ 0\times3 + 0\times2 + 3\times2 + 0\times7 \\ 0\times3 + 0\times2 + 0\times2 + 1\times7 \end{bmatrix} \\ &= \begin{bmatrix} 2\times3 \\ 4\times2 \\ 3\times2 \\ 1\times7 \end{bmatrix} \end{aligned} $
Example 5.
Non square matrices have the same properties:
$ \bs{D}= \begin{bmatrix} 2 & 0 & 0 \\ 0 & 4 & 0 \\ 0 & 0 & 3 \\ 0 & 0 & 0 \end{bmatrix} $
and
$ \bs{x}= \begin{bmatrix} 3 \\ 2 \\ 2 \end{bmatrix} $
$ \bs{Dx}= \begin{bmatrix} 2 & 0 & 0 \\ 0 & 4 & 0 \\ 0 & 0 & 3 \\ 0 & 0 & 0 \end{bmatrix} \times \begin{bmatrix} 3 \\ 2 \\ 2 \end{bmatrix} = \begin{bmatrix} 2\times3 \\ 4\times2 \\ 3\times2 \\ 0 \end{bmatrix} $
The invert of a square diagonal matrix exists if all entries of the diagonal are non-zeros. If it is the case, the invert is easy to find. Also, the inverse doen’t exist if the matrix is non-square.
$ \bs{D}= \begin{bmatrix} 2 & 0 & 0 & 0 \\ 0 & 4 & 0 & 0 \\ 0 & 0 & 3 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} $
$ \bs{D}^{-1}= \begin{bmatrix} \frac{1}{2} & 0 & 0 & 0 \\ 0 & \frac{1}{4} & 0 & 0 \\ 0 & 0 & \frac{1}{3} & 0 \\ 0 & 0 & 0 & \frac{1}{1} \end{bmatrix} $
$ \bs{D}= \begin{bmatrix} 2 & 0 & 0 & 0 \\ 0 & 4 & 0 & 0 \\ 0 & 0 & 3 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \frac{1}{2} & 0 & 0 & 0 \\ 0 & \frac{1}{4} & 0 & 0 \\ 0 & 0 & \frac{1}{3} & 0 \\ 0 & 0 & 0 & \frac{1}{1} \end{bmatrix}= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} $
Let’s check with Numpy that the multiplication of the matrix with its invert gives us the identity matrix:
A = np.array([[2, 0, 0, 0], [0, 4, 0, 0], [0, 0, 3, 0], [0, 0, 0, 1]])
A
array([[2, 0, 0, 0],
[0, 4, 0, 0],
[0, 0, 3, 0],
[0, 0, 0, 1]])
A_inv = np.array([[1/2., 0, 0, 0], [0, 1/4., 0, 0], [0, 0, 1/3., 0], [0, 0, 0, 1/1.]])
A_inv
array([[ 0.5 , 0. , 0. , 0. ],
[ 0. , 0.25 , 0. , 0. ],
[ 0. , 0. , 0.33333333, 0. ],
[ 0. , 0. , 0. , 1. ]])
A.dot(A_inv)
array([[ 1., 0., 0., 0.],
[ 0., 1., 0., 0.],
[ 0., 0., 1., 0.],
[ 0., 0., 0., 1.]])
Great! This gives the identity matrix
Symmetric matrices
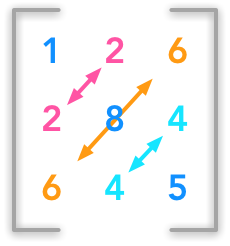Illustration of a symmetric matrix
The matrix $A$ is symmetric if it is equal to its transpose:
$ \bs{A} = \bs{A}^\text{T} $
This concerns only square matrices.
Example 6.
$ \bs{A}= \begin{bmatrix} 2 & 4 & -1 \\ 4 & -8 & 0 \\ -1 & 0 & 3 \end{bmatrix} $
A = np.array([[2, 4, -1], [4, -8, 0], [-1, 0, 3]])
A
array([[ 2, 4, -1],
[ 4, -8, 0],
[-1, 0, 3]])
A.T
array([[ 2, 4, -1],
[ 4, -8, 0],
[-1, 0, 3]])
Unit vectors
A unit vector is a vector of length equal to 1. It can be denoted by a letter with a hat: $\hat{u}$
Orthogonal vectors
Two orthogonal vectors are separated by a 90° angle. The dot product of two orthogonal vectors gives 0.
Example 7.
x = [0,0,2,2]
y = [0,0,2,-2]
plt.quiver([x[0], y[0]],
[x[1], y[1]],
[x[2], y[2]],
[x[3], y[3]],
angles='xy', scale_units='xy', scale=1)
plt.xlim(-2, 4)
plt.ylim(-3, 3)
plt.axvline(x=0, color='grey')
plt.axhline(y=0, color='grey')
plt.text(1, 1.5, r'$\vec{u}$', size=18)
plt.text(1.5, -1, r'$\vec{v}$', size=18)
plt.show()
plt.close()
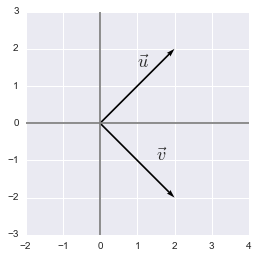Orthogonal vectors
$ \bs{x}= \begin{bmatrix} 2 \\ 2 \end{bmatrix} $
and
$ \bs{y}= \begin{bmatrix} 2 \\ -2 \end{bmatrix} $
$ \bs{x^\text{T}y}= \begin{bmatrix} 2 & 2 \end{bmatrix} \begin{bmatrix} 2 \\ -2 \end{bmatrix}= \begin{bmatrix} 2\times2 + 2\times-2 \end{bmatrix}=0 $
In addition, when the norm of orthogonal vectors is the unit norm they are called orthonormal.
It is impossible to have more than $n$ vectors mutually orthogonal in $\mathbb{R}^n$.
It is impossible to have more than $n$ vectors mutually orthogonal in $\mathbb{R}^n$. For instance try to draw 3 vectors in a 2-dimensional space ($\mathbb{R}^2$) that are mutually orthogonal…
Orthogonal matrices
Orthogonal matrices are important because they have interesting properties. A matrix is orthogonal if columns are mutually orthogonal and have a unit norm (orthonormal) and rows are mutually orthonormal and have unit norm.
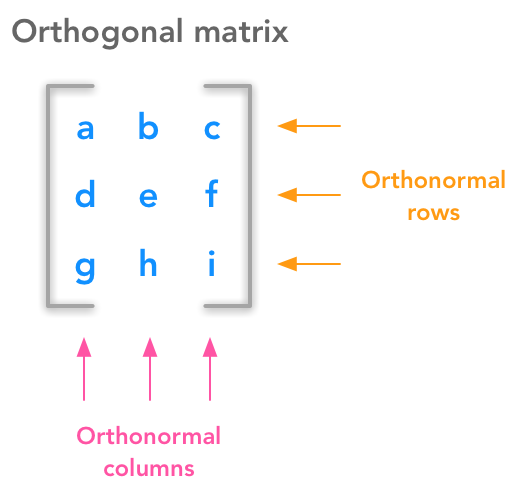Under the hood of an orthogonal matrix
$ \bs{A}= \begin{bmatrix} A_{1,1} & A_{1,2} \\ A_{2,1} & A_{2,2} \end{bmatrix} $
This means that
$ \begin{bmatrix} A_{1,1} \\ A_{2,1} \end{bmatrix} $
and
$ \begin{bmatrix} A_{1,2} \\ A_{2,2} \end{bmatrix} $
are orthogonal vectors and also that the rows
$ \begin{bmatrix} A_{1,1} & A_{1,2} \end{bmatrix} $
and
$ \begin{bmatrix} A_{2,1} & A_{2,2} \end{bmatrix} $
are orthogonal vectors (cf. above for definition of orthogonal vectors).
Property 1: $\bs{A^\text{T}A}=\bs{I}$
A orthogonal matrix has this property:
$ \bs{A^\text{T}A}=\bs{AA^\text{T}}=\bs{I} $
We can see that this statement is true with the following reasoning:
Let’s have the following matrix:
$ \bs{A}=\begin{bmatrix} a & b \\ c & d \end{bmatrix} $
and thus
$ \bs{A}^\text{T}=\begin{bmatrix} a & c \\ b & d \end{bmatrix} $
Let’s do the product:
$ \begin{aligned} &\bs{A^\text{T}A}=\begin{bmatrix} a & c \\ b & d \end{bmatrix} \begin{bmatrix} a & b \\ c & d \end{bmatrix} = \begin{bmatrix} aa + cc & ab + cd \\ ab + cd & bb + dd \end{bmatrix} \\ &= \begin{bmatrix} a^2 + c^2 & ab + cd \\ ab + cd & b^2 + d^2 \end{bmatrix} \end{aligned} $
We saw in 2.5 that the norm of the vector $\begin{bmatrix} a & c \end{bmatrix}$ is equal to $a^2+c^2$ ($L^2$ or squared $L^2$). In addtion, we saw that the rows of $\bs{A}$ have a unit norm because $\bs{A}$ is orthogonal. This means that $a^2+c^2=1$ and $b^2+d^2=1$. So we now have:
$ \bs{A^\text{T}A}= \begin{bmatrix} 1 & ab + cd \\ ab + cd & 1 \end{bmatrix} $
Also, $ab+cd$ corresponds to the product of $\begin{bmatrix} a & c \end{bmatrix} and \begin{bmatrix} b & d \end{bmatrix}$:
$ \begin{bmatrix} a & c \end{bmatrix} \begin{bmatrix} b \\ d \end{bmatrix} = ab+cd $
And we know that the columns are orthogonal which means that:
$ \begin{bmatrix} a & c \end{bmatrix} \begin{bmatrix} b \\ d \end{bmatrix}=0 $
We thus have the identity matrix:
$ \bs{A^\text{T}A}=\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} $
Property 2: $\bs{A}^\text{T}=\bs{A}^{-1}$
We can show that if $\bs{A^\text{T}A}=\bs{I}$ then $ \bs{A}^\text{T}=\bs{A}^{-1}$.
If we multiply each side of the equation $\bs{A^\text{T}A}=\bs{I}$ by $\bs{A}^{-1}$ we have:
$ (\bs{A^\text{T}A})\bs{A}^{-1}=\bs{I}\bs{A}^{-1} $
Recall from 2.3 that a matrix or vector doesn’t change when it is multiplied by the identity matrix. So we have:
$ (\bs{A^\text{T}A})\bs{A}^{-1}=\bs{A}^{-1} $
We also saw in 2.2 that matrix multiplication is associative so we can remove the parenthesis:
$ \bs{A^\text{T}A}\bs{A}^{-1}=\bs{A}^{-1} $
We also know that $\bs{A}\bs{A}^{-1}=\bs{I}$ (see 2.3) so we can replace:
$ \bs{A^\text{T}}\bs{I}=\bs{A}^{-1} $
This shows that
$\bs{A}^\text{T}=\bs{A}^{-1}$
You can refer to this question.
Example 8.
Sine and cosine are convenient to create orthogonal matrices. Let’s take the following matrix:
$ \bs{A}= \begin{bmatrix} cos(50) & -sin(50) \\ sin(50) & cos(50) \end{bmatrix} $
A = np.array([[np.cos(50), -np.sin(50)], [np.sin(50), np.cos(50)]])
A
array([[ 0.96496603, 0.26237485],
[-0.26237485, 0.96496603]])
col0 = A[:, 0].reshape(A[:, 0].shape[0], 1)
col1 = A[:, 1].reshape(A[:, 1].shape[0], 1)
row0 = A[0, :].reshape(A[0, :].shape[0], 1)
row1 = A[1, :].reshape(A[1, :].shape[0], 1)
Let’s check that rows and columns are orthogonal:
col0.T.dot(col1)
array([[ 0.]])
row0.T.dot(row1)
array([[ 0.]])
Let’s check that:
$ \bs{A^\text{T}A}=\bs{AA^\text{T}}=\bs{I} $
and thus:
$ \bs{A}^\text{T}=\bs{A}^{-1} $
A.T.dot(A)
array([[ 1., 0.],
[ 0., 1.]])
A.T
array([[ 0.96496603, -0.26237485],
[ 0.26237485, 0.96496603]])
numpy.linalg.inv(A)
array([[ 0.96496603, -0.26237485],
[ 0.26237485, 0.96496603]])
Everything is correct!
Conclusion
In this chapter we saw different interesting type of matrices with specific properties. It is generally useful to recall them while we deal with this kind of matrices.
In the next chapter we will saw a central idea in linear algebra: the eigendecomposition. Keep reading!
References
Inverse and transpose of orthogonal matrix
Why is the inverse of an orthogonal matrix equal to its transpose
Feel free to drop me an email or a comment. The syllabus of this series can be found in the introduction post. All the notebooks can be found on Github.
This content is part of a series following the chapter 2 on linear algebra from the Deep Learning Book by Goodfellow, I., Bengio, Y., and Courville, A. (2016). It aims to provide intuitions/drawings/python code on mathematical theories and is constructed as my understanding of these concepts. You can check the syllabus in the introduction post.
