Essential Math for Data Science: Visual Introduction to Singular Value Decomposition (SVD)
⥈ ⥈ ⥈Essential Math for Data Science: Eigenvectors and application to PCA
⥈ ⥈ ⥈Essential Math for Data Science: Basis and Change of Basis
⥈ ⥈ ⥈Essential Math for Data Science: Introduction to Systems of Linear Equations
⥈ ⥈ ⥈Essential Math for Data Science: Linear Transformation with Matrices
⥈ ⥈ ⥈Essential Math for Data Science - Introduction to Matrices and the Matrix Product
⥈ ⥈ ⥈Essential Math for Data Science: Scalars and Vectors
⥈ ⥈ ⥈Essential Math for Data Science: Information Theory
⥈ ⥈ ⥈Essential Math for Data Science: The Poisson Distribution
⥈ ⥈ ⥈Essential Math for Data Science: Probability Density and Probability Mass Functions
⥈ ⥈ ⥈Essential Math for Data Science: Integrals And Area Under The Curve
⥈ ⥈ ⥈Essential Math for Data Science: New Chapters
⥈ ⥈ ⥈Essential Math for Data Science
⥈ ⥈ ⥈Deep Learning Book Series 3.4 and 3.5 Marginal and Conditional Probability
⥈ ⥈ ⥈Deep Learning Book Series 3.1 to 3.3 Probability Mass and Density Functions
⥈ ⥈ ⥈Preprocessing for deep learning: from covariance matrix to image whitening
⥈ ⥈ ⥈Deep Learning Book Series · 2.12 Example Principal Components Analysis
⥈ ⥈ ⥈Deep Learning Book Series · 2.11 The determinant
⥈ ⥈ ⥈Deep Learning Book Series · 2.10 The Trace Operator
⥈ ⥈ ⥈Deep Learning Book Series · 2.9 The Moore Penrose Pseudoinverse
⥈ ⥈ ⥈Deep Learning Book Series · 2.8 Singular Value Decomposition
⥈ ⥈ ⥈Deep Learning Book Series · 2.7 Eigendecomposition
⥈ ⥈ ⥈Deep Learning Book Series · 2.6 Special Kinds of Matrices and Vectors
⥈ ⥈ ⥈Deep Learning Book Series · 2.5 Norms
⥈ ⥈ ⥈Deep Learning Book Series · 2.4 Linear Dependence and Span
⥈ ⥈ ⥈Deep Learning Book Series · 2.3 Identity and Inverse Matrices
⥈ ⥈ ⥈Deep Learning Book Series · 2.2 Multiplying Matrices and Vectors
⥈ ⥈ ⥈Deep Learning Book Series · 2.1 Scalars Vectors Matrices and Tensors
⥈ ⥈ ⥈Deep Learning Book Series · Introduction
⥈ ⥈ ⥈
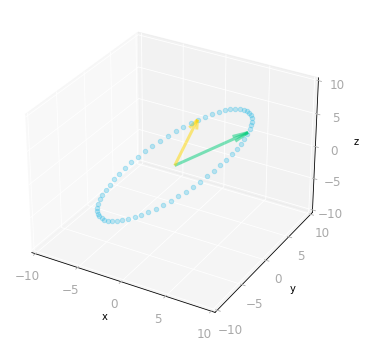 Transformation of the unit circle and basis vectors.
Transformation of the unit circle and basis vectors. 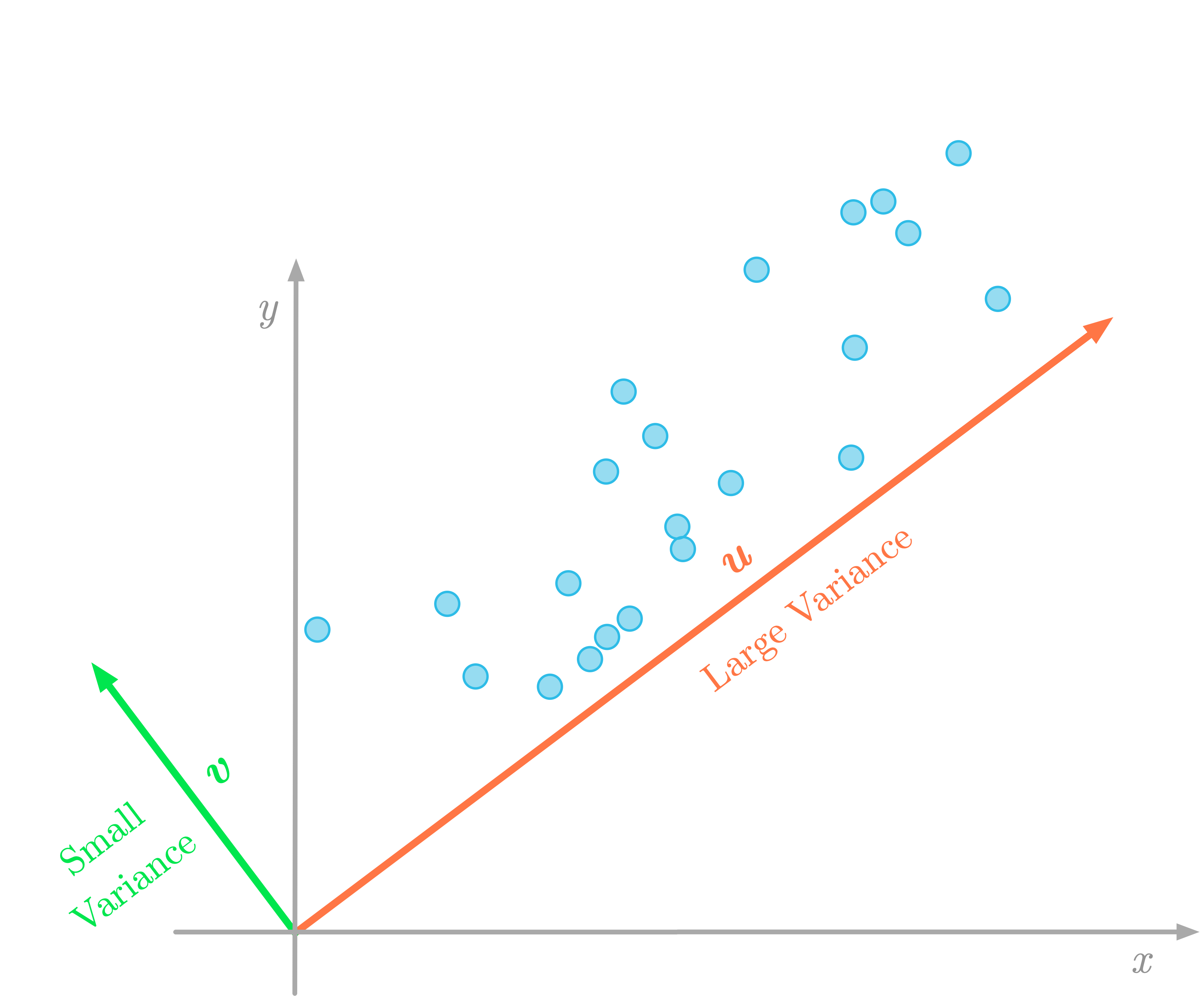 The variance of the data in the direction of the vector $\vu$ (red) is larger than in the direction of the vector $\vv$ (green).
The variance of the data in the direction of the vector $\vu$ (red) is larger than in the direction of the vector $\vv$ (green). 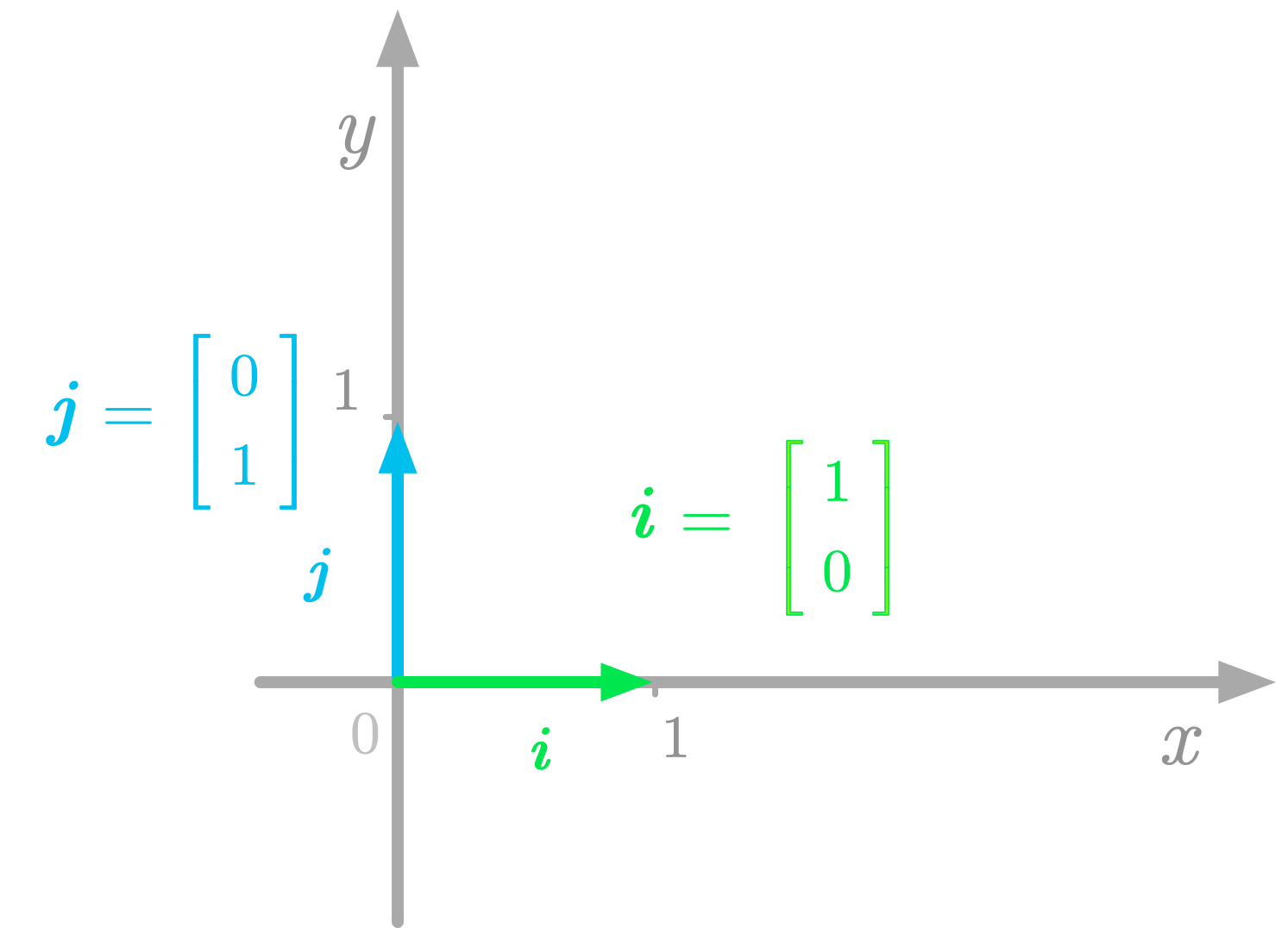 The basis vectors in the Cartesian plane.
The basis vectors in the Cartesian plane. 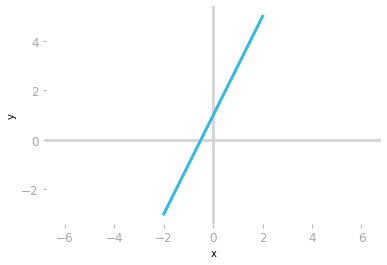 Plot of the equation $y=2x+1$.
Plot of the equation $y=2x+1$. 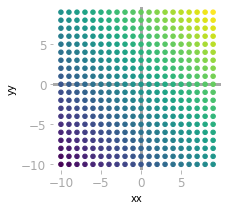 Each point corresponds to the combination of x and y values.
Each point corresponds to the combination of x and y values. 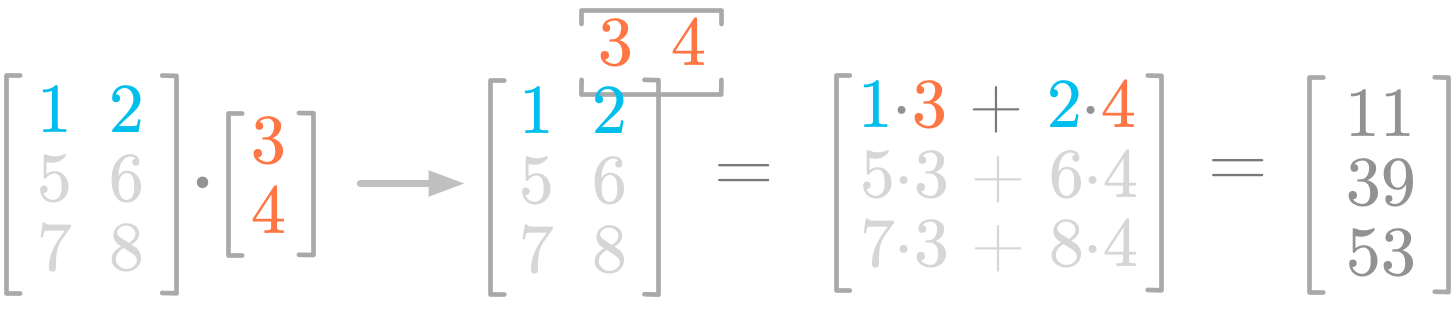 Steps of the product between a matrix and a vector.
Steps of the product between a matrix and a vector.  A geometric vector running from $A$ to $B$.
A geometric vector running from $A$ to $B$. 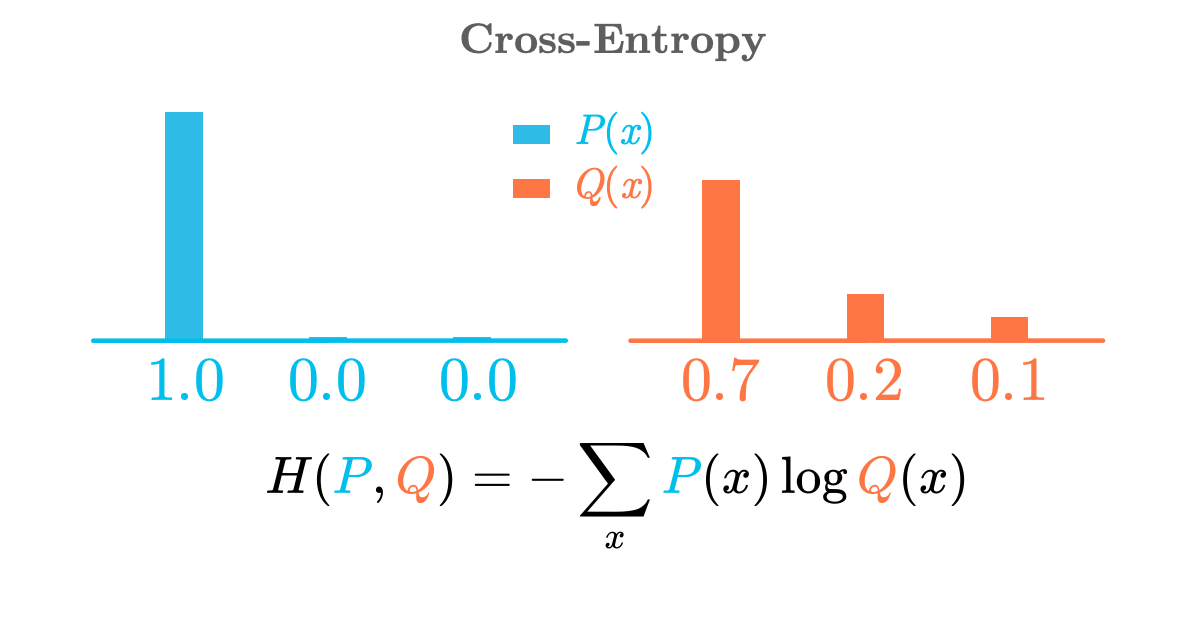 The cross-entropy as a measure of difference between two distributions
The cross-entropy as a measure of difference between two distributions 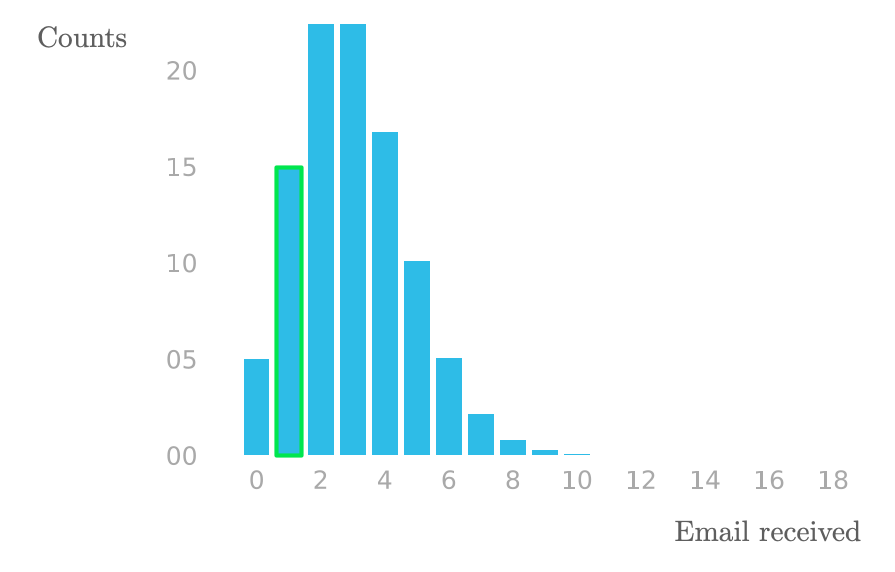 Emails received by Sarah in one-hour intervals for the last 100 hours.
Emails received by Sarah in one-hour intervals for the last 100 hours. 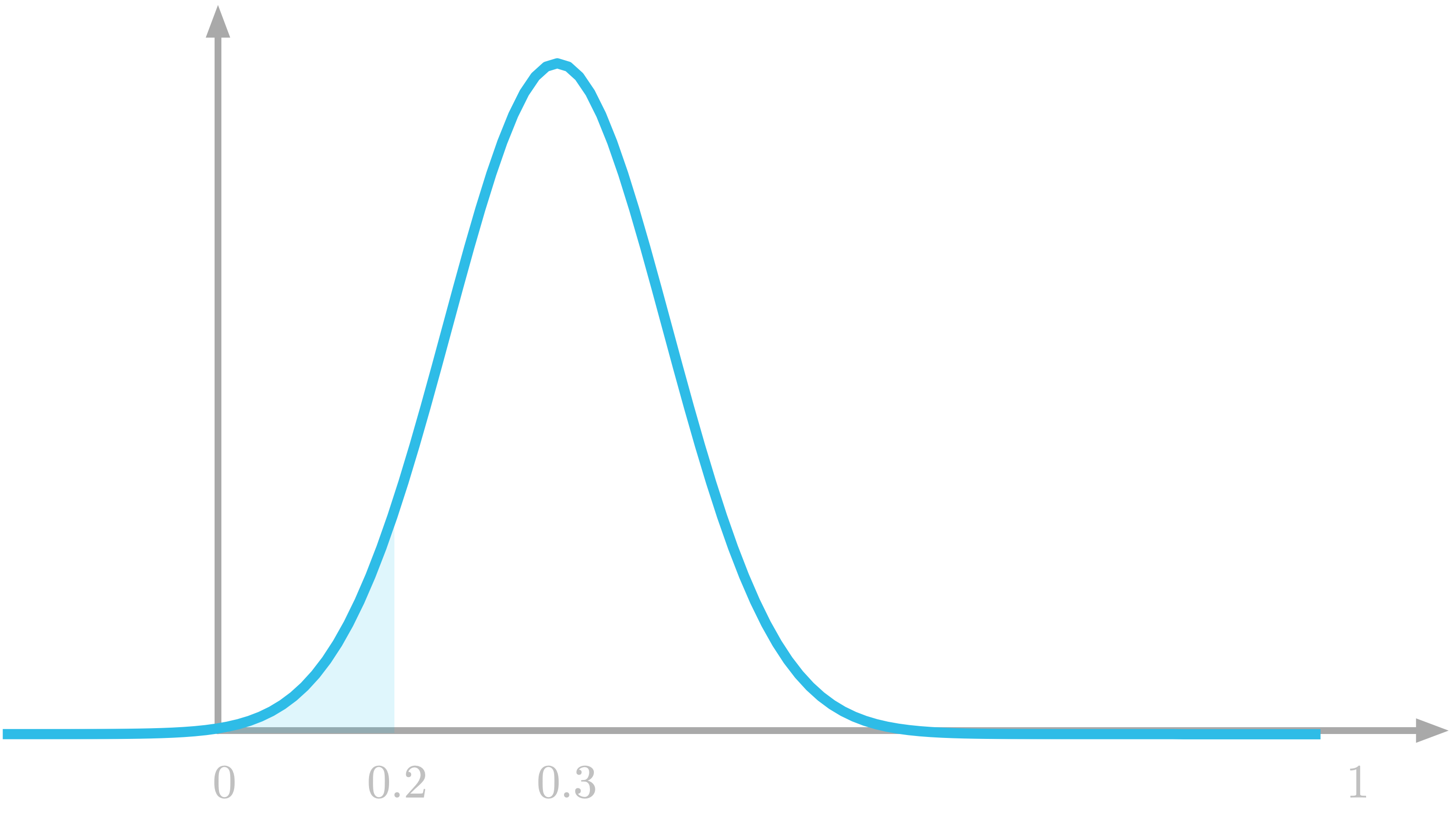 The probability to draw a number between 0 and 0.2 is the highlighted area under the curve.
The probability to draw a number between 0 and 0.2 is the highlighted area under the curve.  Area under the curve.
Area under the curve. 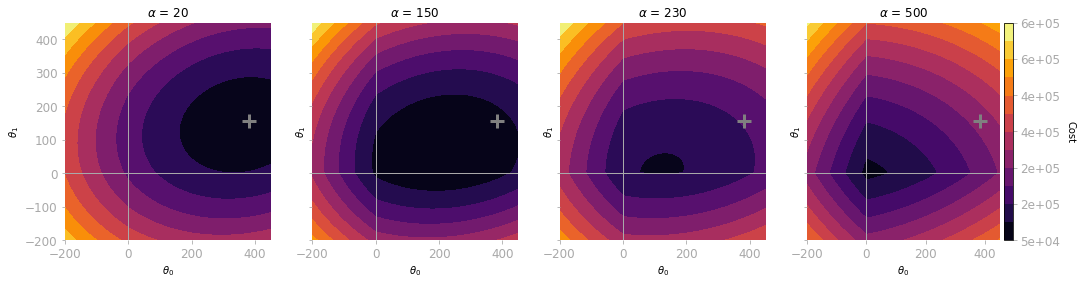 L1 Regularization
L1 Regularization 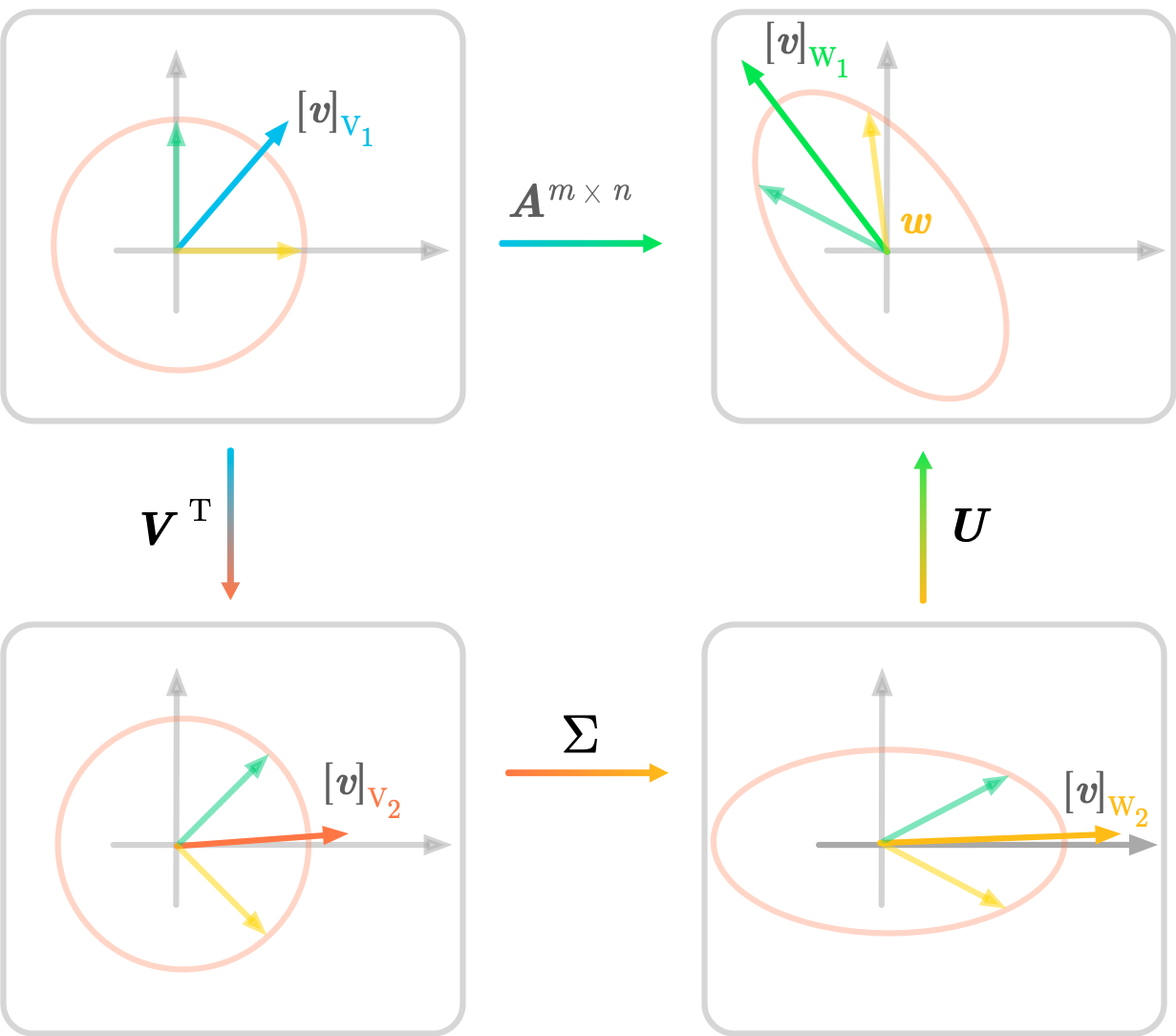 SVD Geometry
SVD Geometry 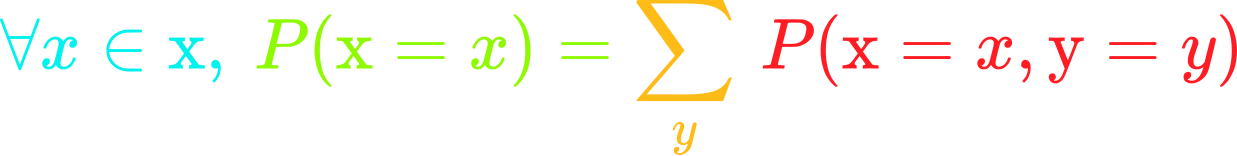 The sum rule allows to calculate marginal probability from joint probability.
The sum rule allows to calculate marginal probability from joint probability.  Probability density function and area under the curve between 0.5 and 0.7.
Probability density function and area under the curve between 0.5 and 0.7. 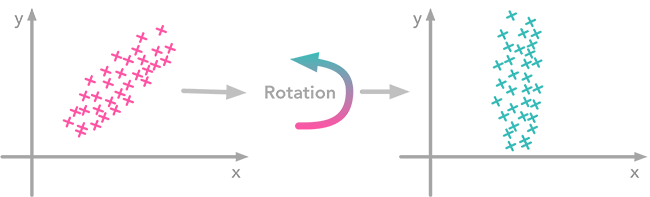 The left plot shows correlated data. For instance, if you take a data point with a big $x$ value, chances are that $y$ will also be quite big. Now take all data points and do a rotation (maybe around 45 degrees counterclockwise): the new data (plotted on the right) is not correlated anymore.
The left plot shows correlated data. For instance, if you take a data point with a big $x$ value, chances are that $y$ will also be quite big. Now take all data points and do a rotation (maybe around 45 degrees counterclockwise): the new data (plotted on the right) is not correlated anymore. 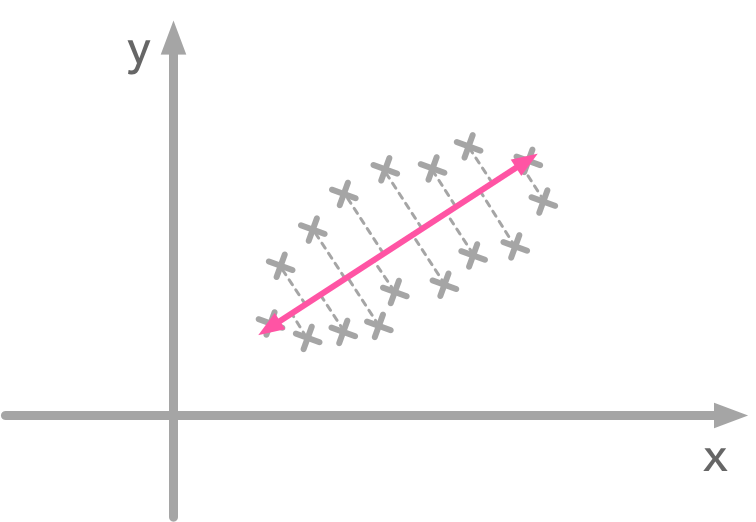 Projection of the data point: the line direction is the one with the largest variance
Projection of the data point: the line direction is the one with the largest variance 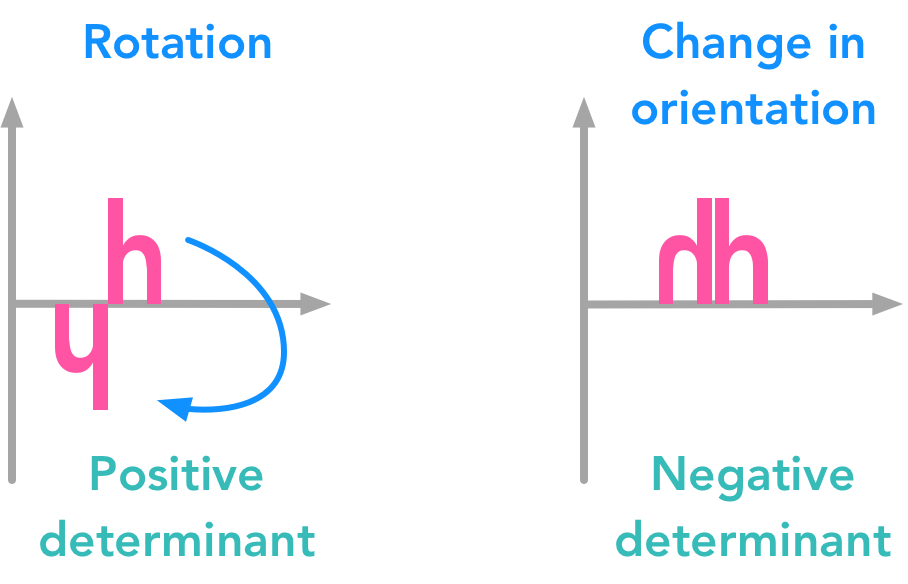 The determinant of a matrix can tell you a lot of things about the transformation associated with this matrix
The determinant of a matrix can tell you a lot of things about the transformation associated with this matrix 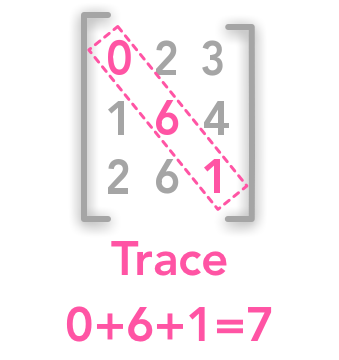 The trace of matrix
The trace of matrix 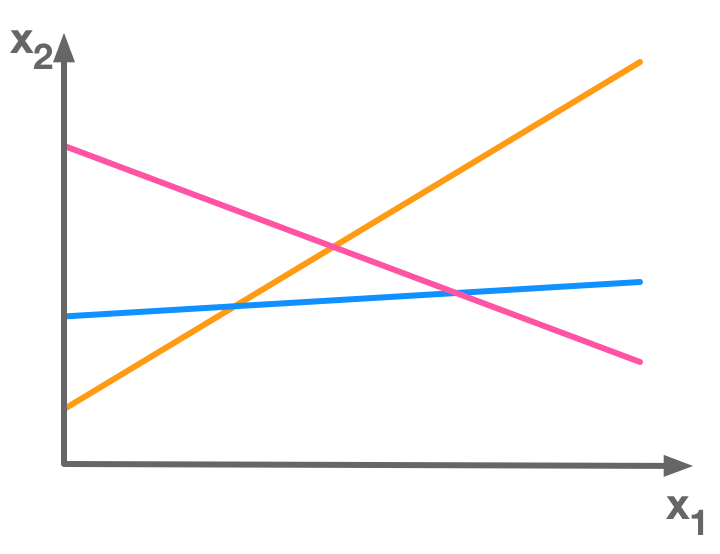 There is more equations (3) than unknowns (2) so this is an overdetermined system of equations
There is more equations (3) than unknowns (2) so this is an overdetermined system of equations 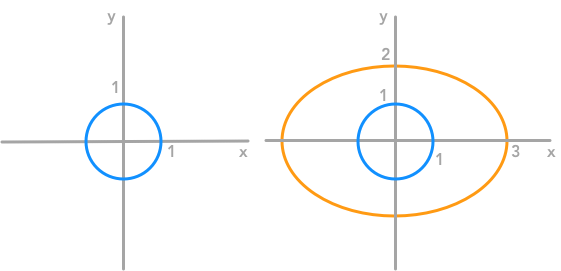 The unit circle and its transformation by a matrix
The unit circle and its transformation by a matrix 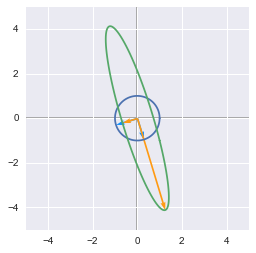 The unit circle and its transformation by the matrix A. The vectors are the eigenvectors of A.
The unit circle and its transformation by the matrix A. The vectors are the eigenvectors of A.  Example of diagonal and symmetric matrices
Example of diagonal and symmetric matrices 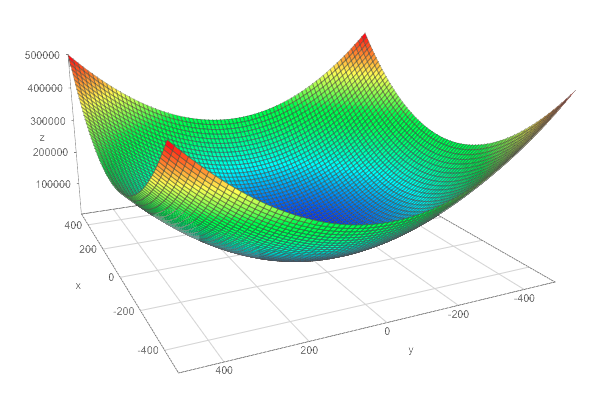 The squared L2 norm
The squared L2 norm 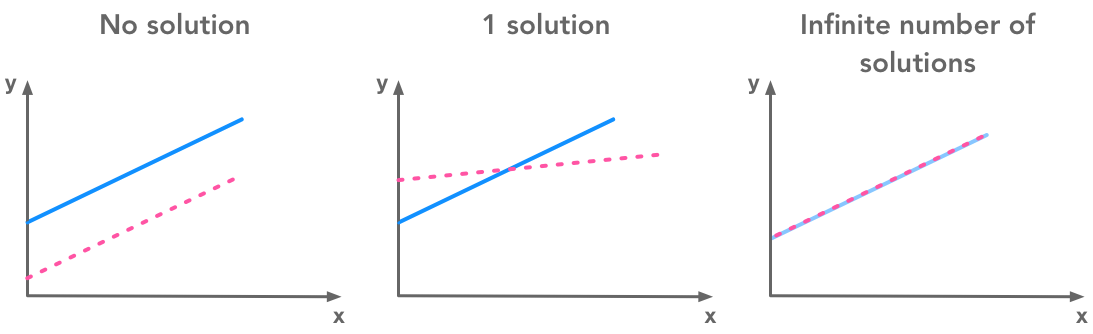 A system of equations has no solution, 1 solution or an infinite number of solutions
A system of equations has no solution, 1 solution or an infinite number of solutions 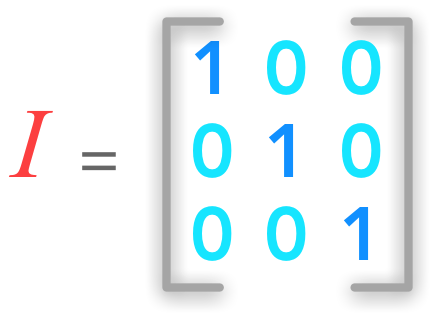 A 3 by 3 identity matrix
A 3 by 3 identity matrix 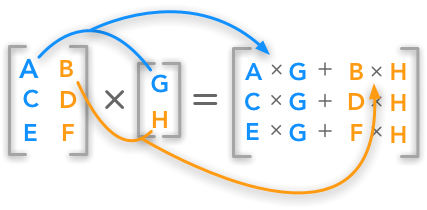 The dot product between a matrix and a vector
The dot product between a matrix and a vector 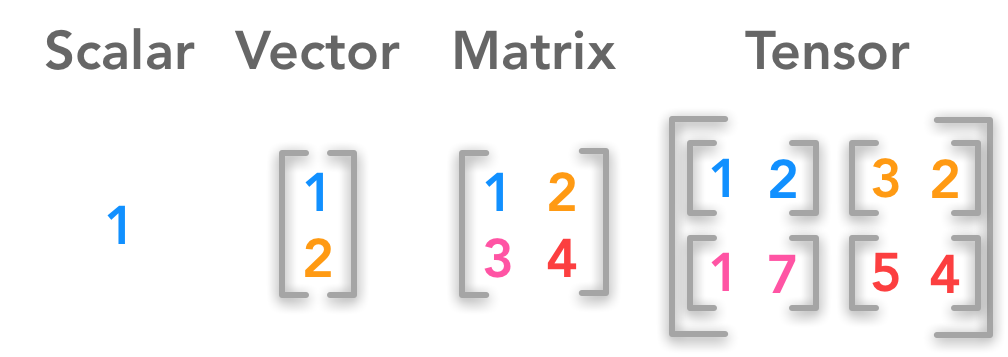 Difference between a scalar, a vector, a matrix and a tensor
Difference between a scalar, a vector, a matrix and a tensor  The Deep Learning Book - Goodfellow, I., Bengio, Y., and Courville, A. (2016)
The Deep Learning Book - Goodfellow, I., Bengio, Y., and Courville, A. (2016)